Happy Pi Day! All around the world today events will be held to celebrate the constant π- for fun and to promote interest in mathematics. We celebrate with the same goal in mind – promoting an interest in mathematics, but we do so through a story. So go grab yourself a slice of π – I mean pie – gather up your children and come right back…
Our story is about a little boy named Andrew who grew up to be a knight. How did a knight get into our math story? Well, maybe math got in our knight story – read on. Andrew lived in England and his father worked at a university – have you ever heard of Oxford? Well, Andrew grew up around and probably in a college sometimes, but he was just a normal boy like you or your brother. He walked back and forth to school just like many other boys in England in the 1950s. But what no one knew – not even Andrew – was that secretly inside he was really a knight!
Sometimes on the way home from school he would stop at the library to look at the books. One day, when he was ten years old, one of those books changed his life forever. It was a book about famous unsolved math problems. Remember, I told you, Andrew was just a normal boy. So just like you or I, he looked at all those math problems that even the world’s greatest mathematicians couldn’t solve and he scratched his head. But just before he put the book back on the shelf one problem caught his eye…
“Hey, that doesn’t look to hard. I’ve seen a problem like that in my math class!” And so Andrew decided he was going to solve this problem. It was called, ‘Fermat’s Last Theorem’.

Pierre de Fermat was a lawyer and an ‘amateur’ mathematician living at the time of Descartes. Photo courtesy of Wikipedia and used under creative commons.
More than 300 years ago there was a mathematician named Pierre de Fermat – actually he was really a lawyer which is how he got the ‘de’ as part of his name, but we won’t hold that against him. Fermat penned a theorem in the margin of a Greek Algebra textbook – yes way back then people wrote in their books, too, even though they were much more precious! It seemed that Fermat wrote about his mathematics a lot – especially in letters to friends. How would you like to get a letter from your friend about math?
What’s a theorem? A theorem is a mathematical statement that declares that something is so – that it is true. This theorem of Fermat’s was a simple theorem – one that even you and I can understand – in fact you most likely have memorized by heart a related theorem: a2 + b2 = c2. Have you heard of Pythagoras? Well, Fermat wondered – if Pythagoras’s theorem is true, is it also true to say a3 + b3 = c3? Or what about a4 + b4 = c4? Is it true for any exponent? We would write that question like this: an + bn = cn. The ‘n’ would stand for all whole numbers – all of them – infinity. That’s a lot of numbers. This is a part of mathematics called number theory.
Fermat said that it wasn’t true. He wrote an + bn ≠ cn but like so much of his other mathematics – Fermat did not show his work – he did not share his proof! Are you asked to show your work in your math? Well, in this case it turned out to be very important because when someone else read that Algebra book and found Fermat’s note – he wasn’t around to explain himself. He had already died. All of his letters and writings were searched but his proof wasn’t there. There was no note in any of the rest of his books…so the mathematicians thought, “No, problem, we’ll just do it ourselves. We’ll find the proof.” Three hundred years later they were still searching and finally gave up, “It’s impossible!” and so they left Fermat’s Last Theorem to sleep.
What’s a proof? Well, it’s very much like being asked to show your work when you solve a problem in your math. Mathematicians often do math in their head just like you, but when they solve a problem or make a discovery that they want to share with other mathematicians, they have to show their work – they have to prove that they did it right. And mathematicians are very competitive – they will try to find a mistake and prove each other wrong!
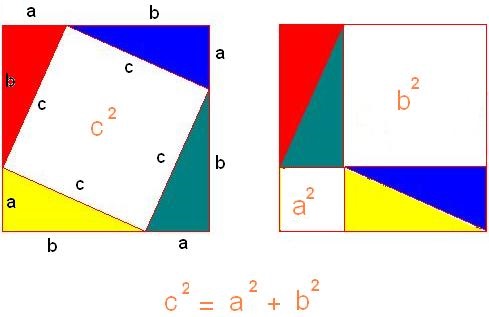
A proof is very much like logic – if I want to prove that 3 + 3 = 5 + 1 how would I do it? It’s not very hard is it? I know that 3+3 = 6 and that 5 + 1 = 6 and it is true to say that 6=6 therefor 3+3 does indeed equal 5+1. So there – you can write a theorem and write a proof. Here is a proof of Pythagoras’s theorem a2 + b2 = c2 :
But let’s get back to Andrew…
I told you that unlike Fermat who didn’t show his work, Andrew was a careful boy. He set about a serious study of mathematics all through his school years. He went to college to study mathematics and even through all of those years he kept before him as his goal to solve Fermat’s theorem. He did not give up. Is he starting to look like a knight yet?

Andrew Wiles at his college graduation. Image courtesy of SimonSingh.net used under creative commons.
In college, after he finished his degree, he decided to keep studying. He picked number theory because that’s the area of math that Fermat’s Last Theorem is a member of. He studied under a professor named John Coates. Coates was a good mathematician. He was also a good man and he liked Andrew. He did not want to see him waste his life trying to solve an unsolvable problem, so he convinced Andrew to give up his dream. Andrew, who was a careful boy, had grown into a careful man, and although it made him sad he saw the wisdom in Coates’ advice. Have you figured out what the dragon in this knight story is yet?

Yutaka Taniyama was a very gifted Japanese mathematician. Image courtesy of Wikipedia and used under creative commons.
Lucky for Andrew, and for you, our story doesn’t end there. Here is where another mathematician who was not very careful comes into our story. Taniyama was a mathematician who lived in Japan. He studied a different part of mathematics than Andrew. He studied elliptical curves. He had a lot of good ideas about elliptical curves but when he wrote his proofs he made mistakes. He had been a little too careless in checking his proof and other mathematicians found the problems. How did he get to be a mathematician if he made so many errors? Do you think that just because you make careless mistakes in your math that you aren’t good at math?
Maybe you just need a friend like Taniyama had. Taniyama’s friend, Shimura, came along beside him and tried to help fix his mistakes and clean up his proof. Shimura said, “Taniyama was not careful. He made a lot of mistakes, but he made them in a good direction.” Shimura knew that without Taniyama’s ideas, he would not be able to go as far in math. And he was right, Shimura was never able to prove Taniyama’s theorem – it remained a conjecture. Shimura said, “It is very hard to make mistakes in a good direction.” But without both Fermat and Taniyama, Andrew would not have been able to go as far in math.
As it turned out Taniyama’s life was sad, but his ideas were very, very important. His theorem connected a lot of areas of math that everyone thought were very different. Other mathematicians made lots of new theorems and they used Taniyama’s ideas – which was called a conjecture because they were not yet proven– in their proofs. This was very risky. If Taniyama was wrong then all of their work was for nothing. It would be as if you had built a tall block tower and your little brother or sister came by and said, “What will happen if I take out this nice big block on the bottom?” Yeah, you know what happens!

Gerhard Frey who also worked with elliptical curves made some discoveries that linked Fermat and Taniyama, but the math world had to wait a couple of years for Ken Ribet to prove the epsilon conjecture. That happened in 1986 Image courtesy of Wikipedia used under the creative commons.
In 1986, which wasn’t so long ago, the math world got really excited. Someone had woken up Fermat’s Last Theorem and it began to fly through the conversations of mathematicians everywhere. Andrew was in his office tower surrounded by his legions of papers and books and files when he heard that the dragon, I mean problem was alive. Another mathematician had entered the fray and woke him up; well maybe that’s exaggerating just a bit but his name was Frey… He said that Taniyama’s conjecture and Fermat’s Last Theorem were linked. Just as we proved that 3 + 3 = 5 + 1, Frey said that if anyone could prove Taniyama’s conjecture then Fermat’s theorem must also be true: Fermat’s Last Theorem = Taniyama’s conjecture.
At last! Andrew, as you can imagine became very excited. There was hope – he would make a plan of attack and figure out how to slay this dragon once and for all. But remember, Andrew was very careful; he didn’t go around telling everyone he was going to solve the problem. He let all the other mathematicians think it was still impossible – after all, neither Taniyama’s nor Fermat’s problems had gotten any easier. He knew that in order to kill the dragon he would need all of his strength and all of his mind and all of his heart. Now he’s sounding like a knight, isn’t he?

Wiles in his office tower. This is a scene from the documentary by Horizons, ‘Fermat’s Last Theorem’. Image courtesy of v2Load used under the creative commons.
So he shut himself into his office tower with his stacks of papers and books and files. Instead of working on any new problems he put all of his time and energy into solving Fermat’s Last Theorem by proving Taniyama’s conjecture. He didn’t do anything except work on the problem and spend time with his wife and children. He thought about it all day long. He thought about it when he went to bed and when he woke up. And he worked. And he worked – for six long years he worked. To keep his secret he published only work that he had already done. Little bit by little bit he would send out a paper or an article that he had already written from his files. No one knew what he was doing except his wife.
After six long years of work he finally found the dragon’s weak spot. He was able to write a proof that showed that Taniyama’s ideas were indeed true. He had to work for another whole year because another mathematician named Richard Taylor said, “It’s not dead yet.” Andrew’s friend Richard had found a problem with his proof. In the end he did find his error and correct it. He is a mathematical hero. I bet you didn’t know math had heroes.

Andrew Wiles and his surprise ending to the lecture he gave where he revealed that he had solved Fermat’s Last Theorem. Image courtesy of SimonSingh.net and used under the creative commons.
It was 1995 and everyone cheered Andrew. He won prizes and was awarded honors but sadly was too old to win Math’s greatest prize, the Fields Medal. The problem had just taken him too long.
But in the year 2000 Andrew was given an honor that confirmed what you and I both already know – he was given his knighthood. He was knighted Knight Commander of the Order of the British Empire!

Sir Andrew Wiles at Cambridge in 2010. Image courtesy of Wikipedia and used under the creative commons.
If you would like to learn about another famous math problem (there are several dragons still alive in math) watch this video over at Numberphile. It has a million dollar prize!
You can also keep an eye on Numberphile’s YouTube channel as they release multiple fun videos about π today!
A note to parents:
This story is of course a simplification. My sources for the most part were Visions of Infinity by Ian Stewart, Wikipedia, and the BBC film Fermat’s Last Theorem. You can watch the film below. I highly recommend it as a good example of what the work of a mathematician is and also a good example of the creative insight that mathematics requires. Do note that the story of Taniyama is sad and involves suicide. This is mentioned in the film briefly but further research can be more graphic.
Fermat’s Last Theorem from Shultz on Vimeo.
If you liked this tell us about it in the comments. If you have other stories of heroes and dragons in math or examples of the art of creativity and imagination in mathematics leave those as well. Would you also consider following us on our Facebook page?